Sự khác biệt giữa tăng gia tốc và gia tốc trung tâm
Nhịp điệu gia tăng so với tốc độ tăng tốc trung tâm
Tăng tốc là tốc độ thay đổi vận tốc, và khi thể hiện bằng cách tính tích phân, đó là thời gian phát sinh của vận tốc. Tăng gia tăng và gia tốc trung tâm là các thành phần của gia tốc cho một hạt hoặc một cơ thể cứng nhắc trong một chuyển động tròn.
Tăng tốc liên tục
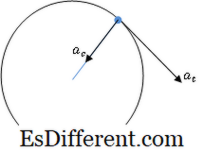
Xem xét một hạt di chuyển dọc theo một con đường như thể hiện trong biểu đồ. Tại trường hợp được xem xét, hạt đang ở góc độ chuyển động, và vận tốc của hạt là tiếp tuyến với con đường.

Tốc độ thay đổi vận tốc tiếp tuyến được định nghĩa là gia tốc tiếp tuyến và được biểu thị bằng t .
->= dv t / dt Tuy nhiên, điều này không tính đến sự gia tốc toàn phần của hạt. Theo luật đầu tiên của Newton, để một hạt đi sai hướng đi và đường thẳng, phải có một lực khác; do đó chúng ta có thể suy luận rằng phải có một thành phần tăng tốc trực tiếp vuông góc với thành phần gia tốc tiếp tuyến, i. e. về phía điểm O tại ví dụ được hiển thị. Thành phần tăng tốc này được gọi là gia tốc bình thường , và được biểu hiện bằng n . ->
/ rNếu u t và u n là các vectơ đơn vị theo hướng tiếp tuyến và tiếp tuyến, sự tăng tốc kết quả có thể được biểu diễn dưới đây.
a = a t u t + n u
n = (dv t / dt) t + (v t 2 / r) u n Tăng tốc hướng tâm Bây giờ xét rằng lực gây ra gia tốc thông thường là hằng số. Trong trường hợp này, hạt đi vào một đường tròn có bán kính r. Đây là trường hợp đặc biệt trong chuyển động góc cạnh, và gia tốc thông thường được cho là gia tốc trung tâm. Lực điều khiển chuyển động tròn gọi là lực trung tâm . Gia tốc trung tâm cũng được biểu diễn ở trên, nhưng mối quan hệ góc cạnh trong vận tốc và gia tốc có thể được sử dụng để cho nó về vận tốc góc. Do đó,
c
= v t 2
/ r = -rω
2
(Ký hiệu tiêu cực cho thấy gia tốc tăng lên chiều ngược lại của vector bán kính) Tăng tốc ròng có thể thu được bằng kết quả của hai thành phần c và t . Sự khác biệt giữa gia tốc tiếp tuyến và tăng tốc tâm là gì?
Tăng tốc tiếp tuyến và tâm là hai thành phần gia tốc của một hạt / thân trong một chuyển động tròn.
• Gia tốc tiếp tuyến là tốc độ thay đổi vận tốc tiếp tuyến, và nó luôn luôn tiếp tuyến với đường tròn, và bình thường với bán kính vector. • Gia tốc tâm được hướng về phía tâm của vòng tròn, và thành phần tăng tốc này là yếu tố chính giữ hạt trong đường tròn. • Đối với một hạt trong chuyển động tròn, vector gia tốc luôn nằm trong đường tròn.




