Sự khác biệt giữa Tích hợp và Tóm tắt: Tích hợp vs Tóm tắt So với
Tổng kết
Trong toán học trung học phổ thông, hội nhập và tổng kết thường được tìm thấy trong các hoạt động toán học. Chúng dường như được sử dụng làm công cụ khác nhau và trong các tình huống khác nhau, nhưng chúng có cùng mối quan hệ rất mật thiết.
Thông tin thêm về Tóm tắt
Tóm tắt là hoạt động của việc thêm một dãy số và hoạt động thường được biểu thị bằng chữ cái của người Hy Lạp sigma Σ. Nó được sử dụng để viết tắt tổng hợp và bằng tổng / tổng số chuỗi. Chúng thường được sử dụng để đại diện cho chuỗi, về cơ bản là các trình tự vô hạn tổng kết. Chúng cũng có thể được sử dụng để chỉ ra tổng của vectơ, ma trận, hoặc đa thức.
Tổng kết thường được thực hiện cho một loạt các giá trị có thể được đại diện bởi một thuật ngữ chung, chẳng hạn như một loạt có một thuật ngữ chung. Điểm xuất phát và điểm kết thúc của tổng kết được gọi là giới hạn dưới và giới hạn trên của tổng kết, tương ứng.
Ví dụ: tổng của dãy 1 , 2 , 3 , 4 , …, a n là 1 + a 2 + 3 + … + n có thể dễ dàng đại diện sử dụng ký pháp tổng kết là Σ n i = 1 a i ; i được gọi là chỉ số tổng kết.
Nhiều biến thể được sử dụng cho tổng kết dựa trên ứng dụng. Trong một số trường hợp, giới hạn trên và giới hạn dưới có thể được cho trong một khoảng hoặc một dải, chẳng hạn như Σ 1≤i≤100 a i và Σ i∈ [1, 100] a i . Hoặc nó có thể được cho là một tập các số như Σ i∈P a i , trong đó P là một tập hợp được xác định.
Trong một số trường hợp, có thể sử dụng hai hoặc nhiều dấu hiệu sigma, nhưng chúng có thể được khái quát như sau: Σ j Σ k jk = Σ j, k a jk .
Ngoài ra, tổng kết theo nhiều quy tắc đại số. Kể từ khi hoạt động nhúng là bổ sung, rất nhiều các quy tắc phổ biến của đại số có thể được áp dụng cho các khoản tiền riêng của mình và cho các điều khoản cá nhân mô tả bởi tổng kết.
Thông tin thêm về Hội nhập
Sự tích hợp được định nghĩa là quá trình đảo ngược sự khác biệt. Nhưng trong hình học của nó nó cũng có thể được coi là khu vực bao bọc bởi các đường cong của các chức năng và trục. Do đó, tính diện tích cho giá trị của một tích phân xác định như thể hiện trong sơ đồ.
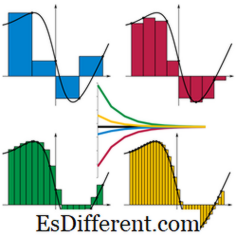
Nguồn hình ảnh: // en. wikipedia. org / wiki / Tập tin: Riemann_sum_convergence. png
Giá trị của tích phân xác định thực sự là tổng của các dải nhỏ bên trong đường cong và trục.Diện tích mỗi dải là chiều cao × chiều rộng tại điểm trên trục được xem xét. Width là một giá trị mà chúng ta có thể chọn, nói Δx. Và chiều cao là xấp xỉ giá trị của hàm tại điểm được quan sát, nói f (x i ). Từ sơ đồ, rõ ràng là các dải nhỏ hơn tốt hơn các dải phù hợp bên trong khu vực bị giới hạn, do đó xấp xỉ tốt hơn giá trị.
Vì vậy, nói chung, tách rời I, giữa các điểm a và b (i. E trong khoảng [a, b] nơi
Δx → 0
Σ n i = 1 f (x i ) Δx = a ∫ b f (x) dx Đây được gọi là Tách Reimann của hàm f (x) trong khoảng [a, b]. Trong trường hợp này a và b được gọi là giới hạn trên và giới hạn dưới của tích phân. Reimann tích phân là một hình thức cơ bản của tất cả các phương pháp hội nhập. Về bản chất, tích hợp là tổng của diện tích khi chiều rộng của hình chữ nhật là vô hạn. Sự khác nhau giữa Tích hợp và Tóm tắt là gì?
• Tóm tắt là thêm của một chuỗi các con số. Thông thường, tổng kết được đưa ra trong mẫu này Σ n i = 1
a
i
khi các thuật ngữ trong dãy có một mẫu và có thể được biểu diễn bằng thuật ngữ chung. • Tích hợp về cơ bản là vùng bị giới hạn bởi đường cong của hàm, trục và giới hạn trên và dưới. Khu vực này có thể được cho là tổng của các khu vực nhỏ hơn nhiều bao gồm trong khu vực có hạn. Tổng kết bao gồm các giá trị rời rạc với giới hạn trên và dưới, trong khi hội nhập bao gồm các giá trị liên tục. • Tích hợp có thể được hiểu như là một dạng tổng kết đặc biệt. • Trong các phương pháp tính toán số, tích hợp luôn được thực hiện như là một tổng kết.




