Sự khác biệt giữa Tích hợp Xác định và Không xác định Hạn định Sự khác biệt giữa
Calculus là một nhánh quan trọng của toán học, và sự khác biệt đóng một vai trò quan trọng trong tích phân. Quá trình nghịch đảo của sự khác biệt được gọi là hội nhập, và ngược lại được gọi là tách rời, hoặc chỉ đơn giản là đưa, sự nghịch đảo của sự khác biệt cho phép tách rời. Dựa trên các kết quả họ tạo ra các phân tích được chia thành hai loại viz., tích phân xác định và không xác định vô hạn.
Xác định tích phân
-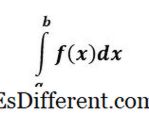
Độ phân giải xác định của f (x) là một SỐ và thể hiện diện tích dưới đường cong f (x) từ x = a đến x = b .
Một tích phân xác định có giới hạn trên và dưới của các phân tích, và nó được gọi là xác định bởi vì, ở phần cuối của vấn đề, chúng ta có một số - đó là một câu trả lời xác định.
Hằng số không xác định của f (x) là một FUNCTION và trả lời câu hỏi "Chức năng nào khi phân biệt chof (x)

? " Với một tích phân vô hạn không có giới hạn trên và dưới của tích phân ở đây, và những gì chúng ta sẽ nhận được là một câu trả lời mà vẫn có trong đó x
và cũng sẽ có một hằng số thường được ký hiệu bởi C ) trong đó.
Giả sử sự khác biệt của hàm
F
dẫn tới một hàm khác f , và sự tích hợp của f cho phép tích phân. Tượng trưng này được viết dưới dạng F (x) = ∫ƒ (x) dx hoặc
F = ∫ƒ dx
ở cả hai
F
và là các chức năng của x , và F là khác biệt. Trong hình thức trên, nó được gọi là một Reimann tách rời và chức năng kết quả đi kèm với một hằng số tùy ý. Một tích phân vô hạn định thường tạo ra một nhóm các chức năng; do đó, tách rời là không xác định. Tích hợp và quy trình hội nhập là trọng tâm của việc giải phương trình vi phân. Tuy nhiên, không giống như các bước khác biệt, các bước tích hợp không phải lúc nào cũng theo một quy trình rõ ràng và chuẩn. Đôi khi, chúng ta thấy rằng giải pháp không thể được thể hiện rõ ràng về chức năng cơ bản. Trong trường hợp đó, giải pháp phân tích thường được đưa ra dưới dạng một tách rời không xác định. Định lý cơ bản của Calculus
Sự tách rời xác định và không xác định được kết nối bởi Định lý cơ bản của Calculus như sau: Để tính
tích phân xác định
, tìm
tách rời không xác định > (còn được gọi là chống dẫn xuất) của chức năng và đánh giá tại các điểm cuối x = a và x = b . Sự khác biệt giữa tích phân xác định và không xác định vô hạn sẽ hiển nhiên khi chúng ta đánh giá tích phân cho cùng một chức năng. Xem xét các tích phân sau đây: OK. Hãy cùng làm cả hai và nhìn thấy sự khác biệt. Để tích hợp, chúng ta cần phải thêm vào một chỉ mục dẫn chúng ta tới biểu thức sau:
Tại thời điểm này
C

chỉ là một hằng số đối với chúng ta. Cần thêm thông tin trong vấn đề để xác định giá trị chính xác
C
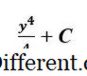
. Hãy để chúng tôi đánh giá sự tách rời tương tự trong hình thức xác định của nó i. e., với giới hạn trên và dưới bao gồm. Nói một cách đồ hoạ, bây giờ chúng ta tính diện tích dưới đường cong f (x) = y 3
giữa

y = 2 và y = 3 >. Bước đầu tiên trong đánh giá này giống như đánh giá tách rời không xác định. Sự khác biệt duy nhất là thời gian này xung quanh chúng ta không thêm hằng C . Biểu hiện trong trường hợp này như sau: Điều này dẫn đến:
Về cơ bản, chúng ta đã thay thế 3 và sau đó là 2 trong biểu thức và nhận được sự khác biệt giữa chúng. Đây là giá trị xác định như trái ngược với việc sử dụng C
hằng

trước đó.

Chúng ta hãy tìm hiểu một số chi tiết hơn về các yếu tố liên tục (liên quan đến tách rời vô hạn).
Nếu sự khác biệt y 3
là
3y 2 , sau đó ∫ 3y 2 dy = y
3 Tuy nhiên 3y 2 có thể là sự khác biệt của nhiều biểu thức, trong đó có
y 3 -5 , > y 3 +7 , vv.. Điều này ngụ ý rằng sự đảo ngược không phải là duy nhất vì không đổi liên tục trong quá trình vận hành. Như vậy, nói chung, 3y 2 là chênh lệch y
3 + C ở đó C là bất kỳ hằng số. Ngẫu nhiên, C được biết đến như là hằng số tích hợp . Chúng tôi viết cái này như sau: ∫ 3y 2. dx = y
3
+ C Các kỹ thuật tích hợp cho tích phân vô thời hạn, chẳng hạn như tra cứu bảng hoặc tích hợp Risch, có thể bổ sung các gián đoạn mới trong quá trình tích hợp. Những sự không liên tục mới xuất hiện bởi vì các dẫn xuất chống lại có thể yêu cầu đưa ra các logarithms phức tạp. Các logariths phức tạp có một sự gián đoạn liên tục khi đối số đi qua trục thực âm, và các thuật toán hội nhập đôi khi không thể tìm thấy một biểu diễn nơi các bước nhảy này bị hủy bỏ. Nếu tích phân định rõ được đánh giá bằng cách tính toán một lần tích phân vô hạn định và sau đó thay thế các ranh giới tích hợp vào kết quả, chúng ta phải biết rằng tích hợp không định hạn có thể tạo ra sự gián đoạn. Nếu có, thêm, chúng ta phải điều tra sự gián đoạn trong khoảng thời gian tích hợp.



