Sự khác biệt giữa Centroid Circumcenter Incenter và Orthocenter | Centroid vs Circumcenter vs Incenter và Orthocenter
Circumcenter, Incenter, Orthocenter và Centroid
Circumcenter: circumcenter là điểm giao nhau của ba các đường phân giác vuông góc của tam giác . Circumcenter là trung tâm của circumcircle , là một vòng tròn đi qua cả ba đỉnh của một tam giác.

Để vẽ circumcenter tạo ra bất kỳ hai bisectors vuông góc với các cạnh của tam giác. Điểm giao điểm cho circumcenter. Một bisector có thể được tạo ra bằng cách sử dụng la bàn và cạnh thẳng của người cai trị. Đặt la bàn đến một bán kính, hơn một nửa chiều dài của đoạn đường. Sau đó, tạo hai vòng cung ở hai bên của đoạn với một kết thúc như là trung tâm của cung. Lặp lại quy trình với đầu kia của đoạn. Bốn đường cung tạo hai điểm giao điểm ở hai bên của đoạn. Vẽ một đường nối hai điểm này với sự trợ giúp của thước đo, và nó sẽ cho phép phân chia vuông góc của đoạn.
Để tạo circumcircle, vẽ một vòng tròn với circumcenter làm trung tâm và chiều dài giữa circumcenter và đỉnh là bán kính của vòng tròn.
Nhú vào:
Nhện là điểm giao giữa ba góc phân nửa s . Incenter là trung tâm vòng tròn với chu vi giao nhau với cả ba mặt của tam giác.
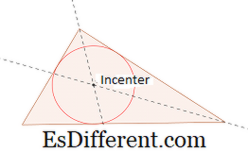
bên trong của tam giác . Các điểm giao nhau của hai góc phân chia cho các incenter. Để vẽ mặt cắt góc, tạo hai vòng cung trên mỗi cánh tay với cùng một bán kính. Điều này cung cấp hai điểm (một trên mỗi cánh tay) trên cánh tay của góc. Sau đó lấy từng điểm trên cánh tay làm trung tâm, vẽ thêm hai cung nữa. Điểm được xây dựng bởi giao điểm của hai cung cung cấp cho một điểm thứ ba. Một đường nối điểm đỉnh của góc và điểm thứ ba cung cấp cho góc phân đôi. Để tạo
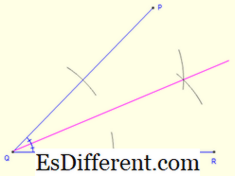
đường tròn , hãy xây dựng một đoạn thẳng vuông góc với bất kỳ cạnh nào đi qua ống lót. Lấy chiều dài giữa chân đế vuông và ống lót làm bán kính, vẽ một vòng tròn hoàn chỉnh. Orthocenter:
Orthocenter là điểm giao nhau của ba chiều cao (độ cao) của tam giác. Để tạo orthocenter, vẽ bất kỳ hai

độ cao của một tam giác . Một đoạn thẳng vuông góc với một cạnh đi qua đầu đỉnh đối lập được gọi là chiều cao.Để vẽ một đường thẳng vuông góc đi qua một điểm, đầu tiên đánh dấu hai đường cung trên đường thẳng với điểm là tâm. Sau đó, tạo thêm hai vòng cung với mỗi điểm giao nhau làm trung tâm. Vẽ một đoạn thẳng nối điểm đầu và điểm cuối cùng được xây dựng, và cho đường thẳng vuông góc với đoạn thẳng và đi qua điểm đầu tiên. Điểm giao điểm của hai cao cho các orthocenter. Centroid:
Centroid là điểm giao nhau của ba trung vị của một tam giác . Centroid chia mỗi trung vị thành tỷ lệ 1: 2, và trung tâm của khối tam giác đồng nhất, tam giác nằm ở điểm này. Để xác định centroid, hãy tạo ra hai trung vị của tam giác. Để tạo trung vị, đánh dấu điểm giữa của một bên. Sau đó xây dựng một đoạn thẳng nối giữa điểm và đỉnh đối lập tam giác. Điểm giao điểm của các trung vị cho centroid của một tam giác.

Sự khác biệt giữa Circumcenter, Incenter, Orthocenter và Centroid là gì?
• Circumcenter được tạo ra bằng cách sử dụng các bisectors vuông góc của tam giác.
• Khởi động được tạo ra bằng cách sử dụng các góc cạnh của các tam giác.
• Orthocenter được tạo ra bằng cách sử dụng chiều cao (độ cao) của tam giác.
• Centroid được tạo ra bằng cách sử dụng trung vị của tam giác.
• Cả circumcenter và incenter đều có các đường tròn với các đặc tính hình học cụ thể.
• Centroid là trung tâm hình học
của tam giác , và là trung tâm của khối lượng của một lớp tam giác đồng nhất. • Đối với một tam giác không đều, circumcenter, orthocenter, và centroid nằm trên một đường thẳng, và đường được gọi là đường
Euler .




